¿Cómo acomodar una infinidad de cosas en un espacio infinito? Este miércoles Juan de Pedazos de Carbono nos lo explica y nos cuenta acerca de un hotel que, aunque tenga muchísimos huéspedes, siempre tiene habitaciones disponibles.
--
Hace ya un buen rato que iniciamos nuestro recorrido por la tierra de los números, familiarizándonos con especies que parecían tan exóticas como los números negativos, los quebrados, los irracionales e incluso los imaginarios y los complejos. Pero el día de hoy regresaremos a repasar esa idea básica y fundamental de la que se desprenden todos los números: la idea de contar.
¿Qué cosa es contar? Así como humanos hace 50,000 años verificaban la regularidad de los ciclos lunares, contar es la simple acción de relacionar los elementos de un grupo de cosas (puestas de sol, patos o manzanas) con los elementos de otro grupo (las marcas talladas en un hueso, piedras o panqués). Si podemos establecer esta relación entre dos grupos, sin dejar a ningún elemento huérfano ni con más de una pareja, entonces habremos determinado que ambos grupos tienen la misma cantidad de cosas.
Los números surgen entonces como nombres o “etiquetas” que les damos a todas las diferentes cantidades. Por poner un ejemplo sencillo, imaginemos la construcción de un pequeño hotel. Cuando se construye su primer cuarto, al número de habitaciones que tiene le llamamos “uno”. Cuando se construye otra habitación, obtenemos un nuevo número, distinto al anterior, que le llamamos “dos”. Así construímos más habitaciones, y obtenemos números más grandes a los que llamamos “tres”, “cuatro” y, finalmente “cinco”.
Ahora, si en el hotel sólo se admite a una persona por habitación y un día nos encontramos con que todas las habitaciones están llenas, fácilmente podemos concluir que en el hotel deben de haber también “cinco” personas hospedadas. Esto es porque si cada habitación tiene una persona, y cada persona se encuentra asignada a alguna habitación, entonces la cantidad de personas y la cantidad de habitaciones debe de ser la misma. Es bastante sencillo, ¿verdad?
 |
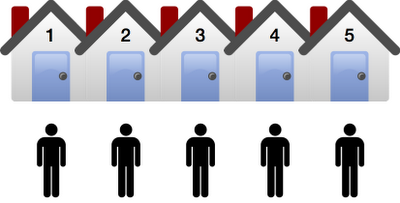| Hay la misma cantidad de habitaciones y de huéspedes: cinco. |
Bien, teniendo esta idea en mente, es tiempo de conocer a David Hilbert, un matemático alemán nacido en 1862 que, aparentemente, en su tiempo libre se dedicaba también a la hotelería. (Esto último es broma, pero síganme la corriente.) A Hilbert le molestaba mucho cuando llegaba a un hotel, tarde por la noche y fatigado después de un largo viaje, sólo para descubrir que el hotel estaba lleno y que no habían más habitaciones disponibles. Ésta es la razón por la cual, cansado de que la gente sufriera de esta clase de rechazos y con el apoyo de un gran número de inversionistas, Hilbert construyó un hotel infinito.
“Bienvenidos al Hotel Hilbert”, aseguran los panfletos y folletos con publicidad, “un lugar encantador, un rostro encantador. Muchas habitaciones en el Hotel Hilbert, en cualquier temporada del año, siempre puedes encontrar.” El hotel en sí—a diferencia de su competencia—no era un hotel muy lujoso. Las habitaciones eran sencillas y tenían los servicios básicos: una TV, una cama individual, un pequeño baño. Sin embargo, para realmente poder cumplir con su promesa, el hotel tenía una cantidad infinita de habitaciones, numeradas comenzando por la “uno”, luego la “dos”, luego la “tres”, ... y así, agregando siempre uno más al número de la habitación anterior. Además, igual como le dimos el nombre “cinco” a la cantidad de habitaciones que tenía el hotel pequeño, diremos que la cantidad de habitaciones que tiene el Hotel Hilbert es “omega”.
 |
| El Hotel Hilbert tiene omega habitaciones, numeradas comenzando por el uno. |
Bueno, pues así pasaron los días, con huéspedes contentos entrando y saliendo del hotel sin nunca preocuparse por si encontrarían alguna habitación disponible. Todo iba perfecto hasta que un día—no me pregunten cómo—el hotel se había llenado por completo. El recepcionista revisaba y confirmaba en los registros que, en efecto, cada habitación estaba registrada al nombre de una persona distinta. Y justo al levantar la vista, todavía un poco incrédulo de la situación, se encontró con que un nuevo huésped caminaba hacia la entrada del Hotel Hilbert.
“¡Oh, no! ¿Pero qué vamos a hacer?”, el recepcionista preocupado llamó inmediatamente a Hilbert para que lo ayudara a resolver la situación. Después de todo, ¿habría que decirle al cliente que no habían ya habitaciones disponibles?
Hilbert escucho las historia del recepcionista, reflexionó por un momento, y finalmente exclamó: “¡No hay ningún problema! Lo único que tenemos que hacer es”, explicó, “pedir a cada huésped que se mueva a la siguiente habitación. El de la habitación 1 se irá a la 2, el de la 2 se irá a la 3, y así sucesivamente. Todos los huéspedes que ya estaban en el hotel seguirán teniendo una habitación y, además, ¡la primera habitación estará vacía para recibir al nuevo huésped!”
 |
| Moviendo a cada huésped un lugar a la derecha, se libera la primera habitación |
A diferencia de lo que que ocurre cuando tienes un grupo de “cuatro” cosas y le agregas otra para obtener un número diferente, el “cinco”; cuanto tienes “omega” personas registradas en un hotel, y agregas una persona más, la cantidad sigue siendo “omega”. Este es un truco bastante simpático que el recepcionista del hotel pronto aprendió a dominar. ¿Llegan “ocho” huéspedes nuevos al hotel cuando está lleno? ¡No hay problema! Sólo pides a cada huésped que se mueva ocho habitaciones a la derecha, todos siguen teniendo una habitación, y las primeras ocho habitaciones quedan disponibles para los nuevos huéspedes. A “omega” le puedes agregar cualquier otro número (finito), y el resultado sigue siendo “omega”.
Pero el recepcionista no estaba preparado para lo que ocurriría después. La popularidad del Hotel Hilbert fue tan grande, que una agencia de viajes le hizo llegar, ¡un autobús infinito cargado con omega personas!
“¡Diantres!”, pensó el recepcionista, “esto debe de ser realmente imposible, ¡donde voy a meter a tanta gente!” Hilbert, sin embargo, como siempre tomando las cosas con calma, reflexionó por un momento hasta que dio con la solución: “¡Ya lo sé! Hagamos que cada uno de los huéspedes en el hotel se vayan a la habitación cuyo número sea el doble de la habitación en la que se encuentran. Por ejemplo, el de la habitación dos se va a la cuatro; el de la tres se va a la seis. Todos los que tienen ahora una habitación seguirán teniendo una habitación, pero ahora ¡todas las habitaciones impares estarán vacías! Y allí podemos registrar a nuestros omega huéspedes nuevos.” Si a un grupo de omega personas le sumas omega nuevas personas, ¡sigues teniendo omega personas!
 |
| Los omega huéspedes anteriores, más los omega huéspedes nuevos, siguen siendo omega |
Ahora sí, pensó el recepcionista, con esta nueva receta, no importa cuanta gente llegue, ¡siempre habrán lugares disponibles para ellos! ¿Que llegan cuatro autobuses repletos y cargados con omega personas? ¡Facilísimo! Que cada huésped multiplique su número de habitación por cinco (para ocupar la cinco, diez, quince, ...); dejando las habitaciones uno a cuatro libres para la primera persona de cada autobús, las habitaciones seis a nueve para la segunda persona de cada autobus, y así sucesivamente. Multiplicar cuatro, o diez, o cinco mil, por omega; sigue dando de resultado omega.
Sin embargo, parece que no era momento aún de cantar victoria. El éxito del hotel fue tan grande, que ahora las agencias de viajes les enviaban ¡omega camiones con omega personas en cada uno! “¿Si le digo a cada huésped que multiplique su número de habitación por omega? ¡No! ¡No hay ninguna habitación omega! ¡Los números en las puertas de las habitaciones son siempre finitos!”, el recepcionista intentaba diversas estrategias sin mucho éxito. “Esto es demasiado, de esta sí que no vamos a poder salir.”
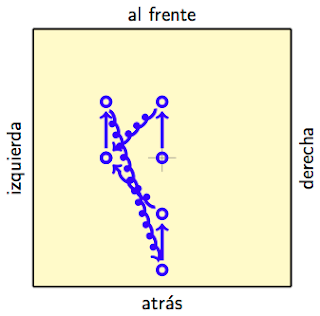
Esta vez al mismo Hilbert le tomó algunos segundos descubrir la solución. Hasta que al final, con una sonrisa, enseñó a su recepcionista el siguiente diagrama que le mostraba como acomodar a todos—a los omega huéspedes que ocupaban ya el hotel, y a los omega autobuses con omega huéspedes nuevos cada uno—en el Hotel Hilbert. En la primera fila acomodó a las omega personas que ya están hospedadas, y el resto de las filas tienen a todas las nuevas personas que llegaron en los omega autobuses nuevos. Las flechas indican el orden en que se puede ir asignando un nuevo número de habitación a todo este montonal de gente. Cuando multiplicas omega por omega, ¡sigues obteniendo omega!
 |
| ... cuando llegan omega autobuses con omega personas cada uno. |
Los lectores avispados notarán que, de hecho, esto también demuestra que la cantidad de números quebrados es igual a omega, la cantidad de números “naturales” que hay. Esto es porque a la persona número “a” que viene en el autobús número “b” la puedes imaginar sosteniendo en sus manos un cartel con el quebrado “a entre b”. El diagrama de arriba muestra como asignar a cada quebrado un número natural. Piensen también que los quebrados eran, de hecho, no sólo infinitos “hacia arriba”, sino también “hacia adentro”: entre cualesquiera dos números, siempre existen más y más números quebrados. Piensen en lo fascinante que es eso: a pesar de ser infinitos en “tantos” sentidos, la cantidad de números quebrados sigue siendo omega.
Y bien, después de tanto éxito, parecería ser entonces que finalmente omega es “el número más grande de todos”. Al fin y al cabo omega es infinito y, no importa cuántos huéspedes más puedan llegar, dentro de este número infinito siempre será posible encontrar más y más habitaciones para hospedarlos, ¿o no?
Pues, aunque no se lo crean, resulta que la respuesta a esta pregunta será el tema de la siguiente entrega en nuestra serie. (Lo ven, les dije que esta serie no se quería acabar.)
Juan
–
Después de analizar los resultados de tus pruebas y los de otros 14 matemáticos voluntarios, Semir documentará la primera evidencia neurobiológica sobre una belleza nunca antes estudiada. Una belleza distinta a la visual, musical o moral que conocemos la mayoría de los seres humanos. Una belleza dependiente de la enseñanza y la cultura. Abstracta. Matemática.
